数据结构
数据结构与算法
树和二叉树部分
完全二叉树和满二叉树
完全二叉树的特点:叶子节点只可能在层数最大的两层出现
对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个
公式总结
已知完全二叉树的总节点数为n求叶子节点个数:
当n为奇数时:(n+1)/2
当n为偶数时 : (n)/2
已知完全二叉树的总节点数为n求父节点个数为:n/2
已知完全二叉树的总节点数为n求叶子节点为2的父节点个数:
当n为奇数时:n/2
当n为偶数时 : n/2-1
具有n个节点的完全二叉树的深度:
$$
h = [log_2n]+1
$$对于任意二叉树,度为0的节点数为$n_0$,度为1的节点数为$n_1$,度为2的节点数为$n_2$,则有
$$
n_0=n_2+1
$$对于有n个节点的的完全二叉树,编号1-n,则对于完全二叉树中编号为i的节点,
若i=1,为根;若2i>n,则该节点无左孩子,否则2i为左孩子;若2i+1>n,该节点无右孩子节点,否则2i+1为右孩子节点n个节点的二叉树中,共有n+1个空指针域
一棵完全二叉树有n个叶子节点,则最多有2n个总节点,最少2n-1个总节点
二叉树的存储结构
链式存储和顺序存储
| leftchild | data | rightchild |
|---|---|---|
| c语言描述 |
1 | typedef struct BitNode{ |
- 几种改进以及常见的表示方法:
- 带有双亲指针的二叉链表,加入一个parent指针域
双亲表示法:
用一组连续的存储空间来存放每个节点,同时每个节点有一个伪指针,指示双亲节点在数组中的尾汁,其中根节点的下标为0,其伪指针域为-1,如图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CBUO0MRM-1613267756201)(https://pad.degrowth.net/uploads/upload_a1078dd5be4549e4ec2dca9e7c06bff8.png)]
代码:
孩子表示法:
将每个节点的孩子节点都用单链表连起来形成一个线性结构,n个节点具有n个孩子链表,如图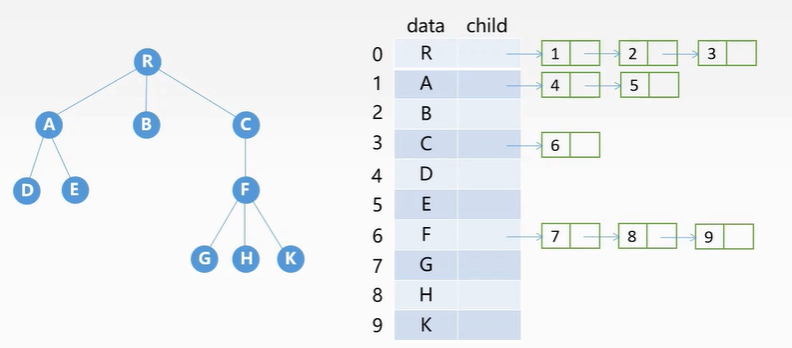
孩子兄弟表示法:
左孩子右兄弟,代码
| 节点的第一个孩子节点指针 | 节点值 | 节点的下一个兄弟节点指针 |
|---|---|---|
| 如图: | ||
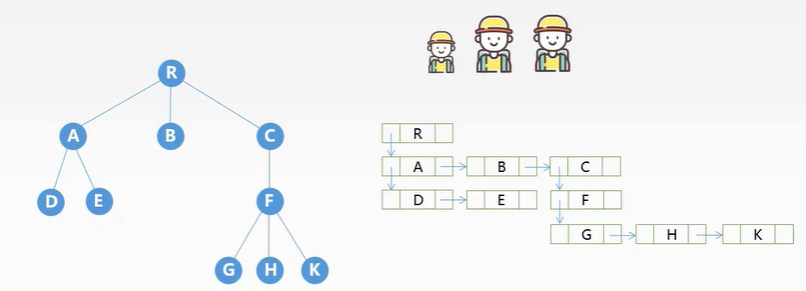 |
总结:
二叉树的遍历(递归算法)
- 先序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
(先判断二叉树非空)
给定前序和后序不能唯一确定二叉树,但只要有中序就行二叉树的遍历(非法递归算法)
博客链接:
https://www.cnblogs.com/pkg313133/p/3459171.html
二叉树的等价与相似
二叉树具有相同结构是指:
- 他们都是空的
- 他们都是非空的,但左右字数具有相同的结构。
定义满足2的为相似二叉树,满足2且相应节点信息相同的为等价二叉树
线索二叉树
中序线索二叉树的遍历:
注意:中序的前驱和后继都指向祖先
前序线索二叉树找前驱困难;中序都差不多,后序找后继困难
树和二叉树,森林的转换
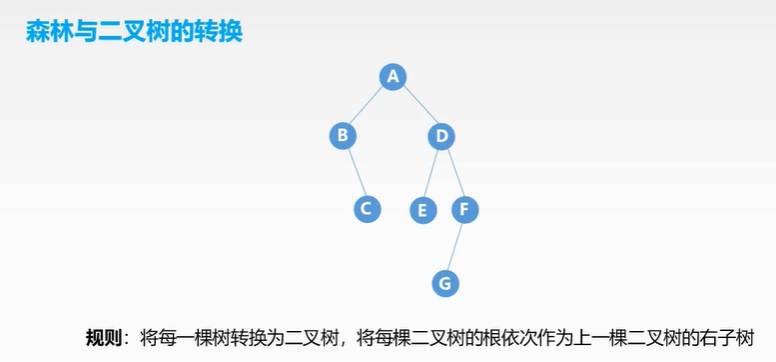
互逆,且转换方式唯一
具体转换方式参照这篇博客:https://blog.csdn.net/tjh625/article/details/87839191
- 森林和树的遍历:与二叉树相似,有先根,后根,层次遍历三种(没有中根)
树的先根遍历和这棵树对应的二叉树的先序遍历相同;
树的后根遍历序列与这棵树对应二叉树的中序遍历相同
森林的先序遍历就是依次对应二叉树进行先根遍历,森林的中序遍历就是对与森林对应二叉树的中序遍历 - 相关链接:https://blog.csdn.net/linraise/article/details/11745559
树的应用
二叉排序树(二叉查找树)BST
性质:每个节点,若左子树非空,左子树的所有节点关键值均小于该节点,右子树关键值均大于该节点(是一种递归结构)
对二叉排序树进行中序遍历,可得到一个递增的有序序列,查找效率非常高
- 二叉树的一些操作
- 查找

- 插入
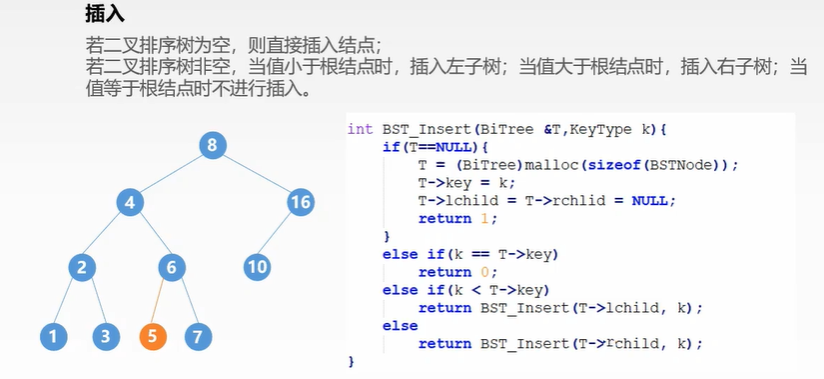
- 构造
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zArGtbAZ-1613267756215)(https://pad.degrowth.net/uploads/upload_aASL1856c20f88157f83b7f43416db3f757.png)] - 删除
- 若被删除节点是叶子节点,直接删除
- 若被删除节点只有一颗子树,则让z的子数成为z父节点的子树(长子继承)
- 若被删除节点有两颗子树,则让z的中序序列的直接后继代替z,并删除直接后继节点(难)
注意:二叉排序树中删除并插入某节点,得到的二叉排序树和原来不一定相同。
二叉排序树最大元和最小元不一定是叶子
5. 查找效率(ASL)
平均查找长度取决于树的高度
ASL = 每个节点的层次相加最后取平均
平衡二叉树的查找效率最高
霍夫曼树
n个叶子节点的二叉树,每个叶子节点带权,则必存在一棵带权路径长度WPL最小的树,成为霍夫曼树。
$$
带权路径长度(WSL)= \sum w_i\times L_i
$$

平衡二叉树(AVL)
性质:左右子树高度差绝对值不超过1
高度为h的最小(节点数最少)平衡二叉树的节点数$N_h$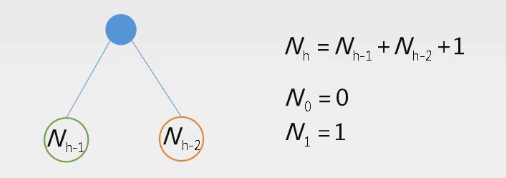
AVL旋转操作:https://blog.csdn.net/qq_24336773/article/details/81712866
图
基本概念
顶点(Vertex)、弧(Arc)、弧头(初始点)、弧尾(终结点)、边(Edge)、有向图(Directed graph)、无向图(Undigraph)、完全图(Completed grapg)、有向完全图、稀疏图(Sparse graph)、稠密图(Dense graph)、连通、连通图(Connected graph)、连通分量(Connected Component)、强连通图、强连通分量(有向图中的极大强连通子图)、生成树、极小连通子图、有向树。
无向图:G=(V, {E})、0≤边≤n(n-1)/2
有向图:G=(V, {A})、0≤弧≤n(n-1)
连通图:在无向图G中,如果图中任意两个顶点vi, vj属于V,vi和vj都是连通的,则图G是连通图。
连通分量:无向图中的极大连通子图
强连通图:在有向图G中,如果每一对顶点vi, vj属于V且vi不等于vj,从vi到vj与从vj到vi都存在路径,则图G是连通图。
强连通分量:有向图的极大强连通子图。
生成树:一个连通图的生成树是一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的n-1条边。
如果在生成树上添加一条边,必定构成一个环:因为这条边使得它依附的那两个顶点之间有了第二条路径。
一个有n个顶点的生成树有且仅有n-1条边。如果一个图有n和顶点和小于n-1条的边,则是非连通图。如果多余n-1条边,则一定有环。但有n-1条边的图不一定是生成树。
博客:https://blog.csdn.net/u013071074/article/details/28308275邻接矩阵
用两个数组来表示图。一个一维数组存储图中数据元素(顶点)的信息,一个二维数组(邻接矩阵)存储图中数据元素之间的关系(边或弧)的信息。
邻接表法:

注意:无向图的邻接表中,每一条无向边要被存储两次(因为单一有方向)如图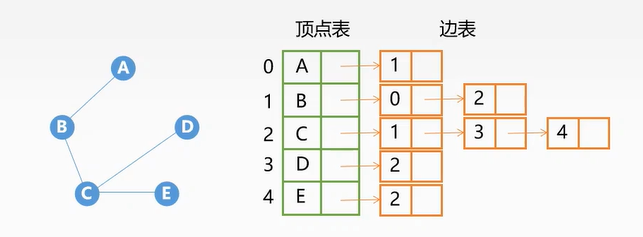
代码实现: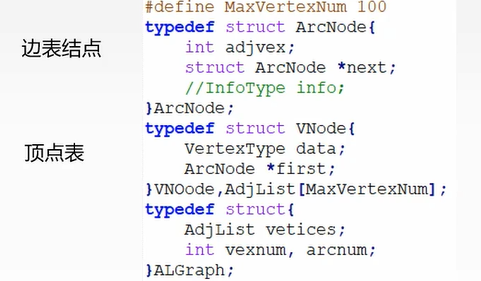
若G为无向图,存储空间为O(|V|+2|E|)
若G为有向图,存储空间为O(|V|+|E|)

两种存储结构对比:邻接表优于邻接矩阵十字链表法(比较复杂)
博文:https://blog.csdn.net/bible_reader/article/details/71214096
图的基本操作
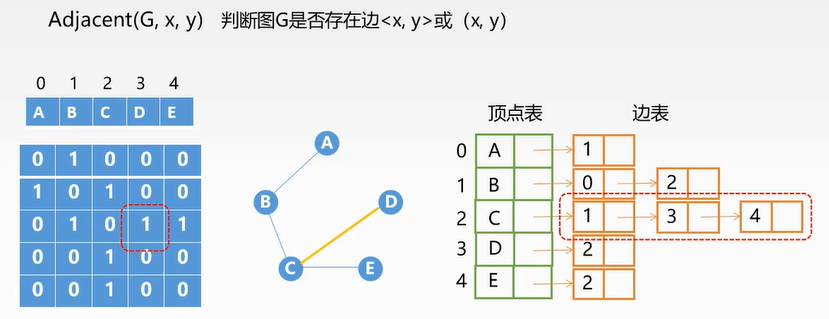
矩阵优于链表(无论是有向图还是无向图)

链表优于矩阵(无向图),有向图反之
插入点操作(Insert(G,x))删除点操作(Delete(G,x))
对应修改相应的邻接矩阵和邻接表即可。
深度优先算法
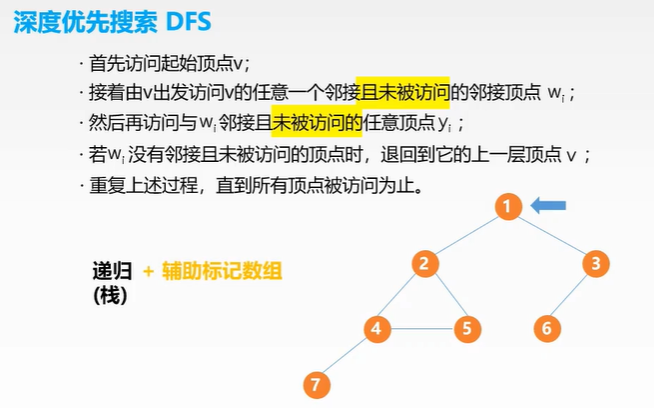
代码:
1 | bool visited[MAX_TREE_SIZE] |
算法性能分析:空间复杂度:O(|V|)
时间复杂度:
| 邻接矩阵 | O(V^2)|
| ——– | ——–| ——– |
| 邻接表法 | O(V+E)|
广度优先算法
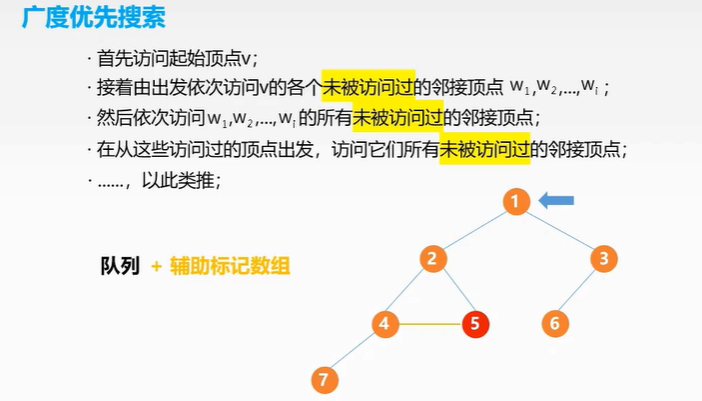
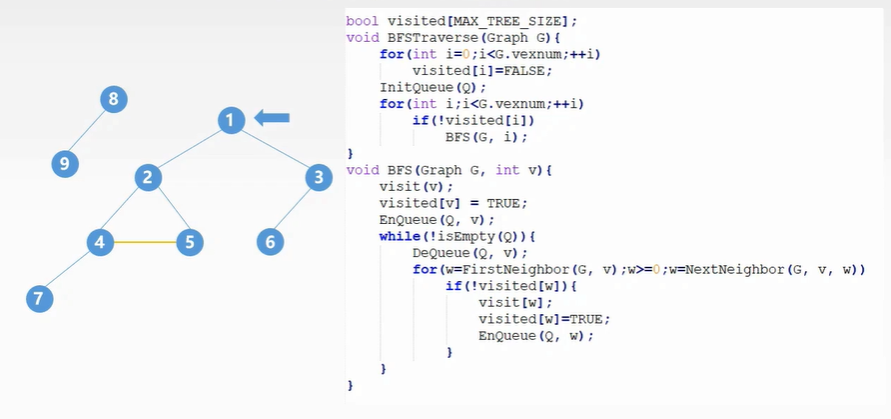
BFSTraverse的作用是针对那些没有联通的顶点进行遍历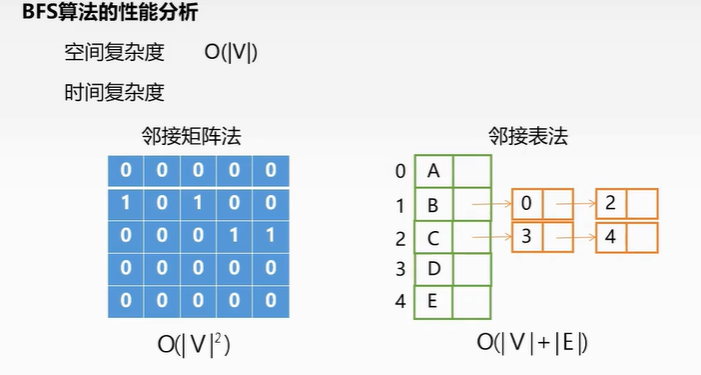
最小生成树
- 性质:图的最小生成树不一定唯一(唯一的情况是各边权值不等)
- 最小生成树算法:
prim算法(防止了环的生成)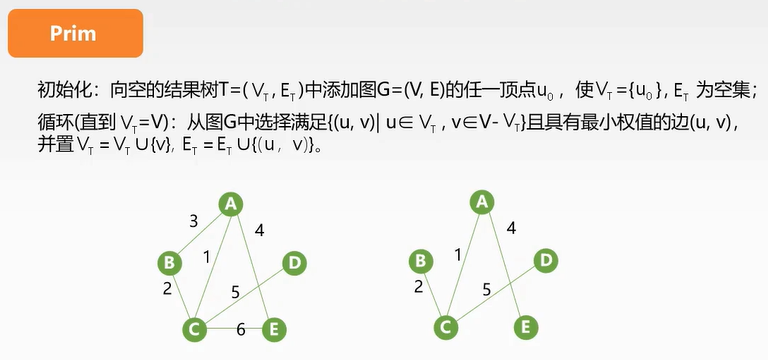
两个数组:min_weight记录边的权值(全部为0,生成结束) adjvex记录U集合中的顶点(该点上一个点的下标)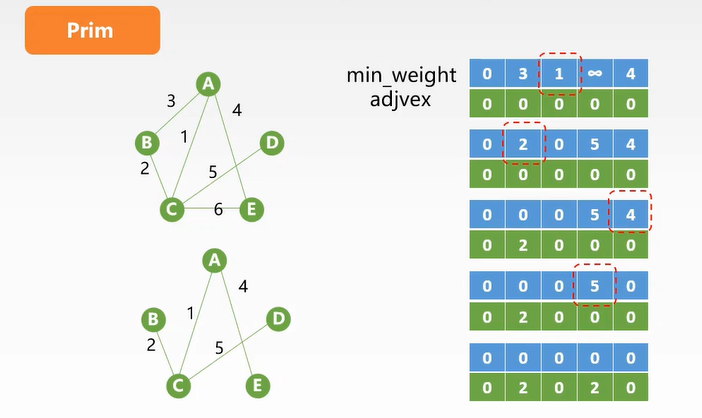
代码如下:(O|$n^2$|)适合稠密图1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30void MST_Prim(Graph G)
{
int min_weight[G.vexnum];
int adjvex[G.vexnum];
for(int i = 0;i<G.vexnum;i++)
{
min_weight[i] = G.edge[0][i];
adjvex[i] = 0;
}
int main()
{
int min_arc;
int min_vex;
for(int i = 1;i<G.vexnum;i++){
min_arc = MAX;
for(int j = 1;j<G.vexnum;j++)
if(min_weight[j]!=0&&min_weight[j]<min_arc){
min_arc = min_weight[j];
min_vex = j;
}
}
min_weight[min_vex] = 0;
for(int j = 0;j<G.vexnum;j++){
if(min_weight[j]!=0&&G.edge[min_arc][j]<min_weight[j]){
min_weight[j]=G.efge[min_arc][j];
adjvex[j] = min_vex;
}
}
}
}
Kruskal算法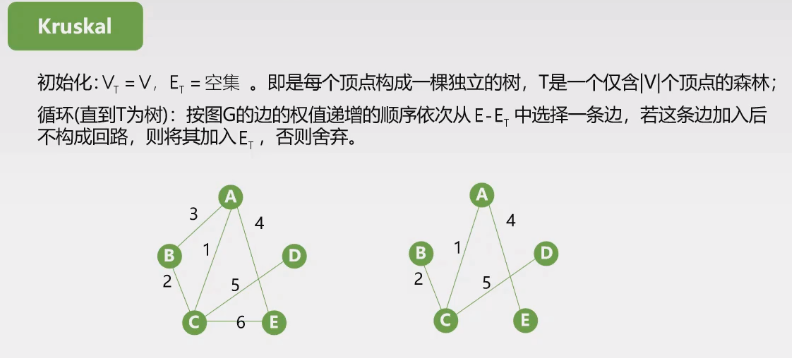
代码:
适合于稀疏图,复杂度O(eloge)(e为边)
有向无环图(DAG)
- 不存在环的有向图
- AOV网:用DAG表示一个工程,顶点表示活动,<vi,vj>表示活动传递关系的网络
- 拓扑排序:对DAG所有顶点的排序,使得若存在一条从顶点A到顶点B的路径,在排序中B排在A后面

一个有向无环图拓扑排序序列不一定唯一;有向有环图无拓扑序列
如果顶点还未输出完就已经找不到入度为0的顶点,说明有环,退出 代码:(用一个栈辅助)  复杂度(O|V|+|E|) 结论:若邻接矩阵为三角矩阵,则存在拓扑排序;反之不一定成立 Indegree函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15//求各顶点入度的程序
void FindInDegree(ALGraph G, int indegree[])
{
int i;
ArcNode *p;
for (i = 0; i < G.Vexnum; i++)
{
p = G.Vertices[i].firstarc;
while (p)
{
indegree[p->adjvex]++;
p = p->next;
}
}
}
关键路径
- 概念:(AOE网)带权有向图,边表示活动,权表示持续时间(一般)
- 特点:只有一个出度为0的点(汇点),一个入度为0(源点)
- 最短时间是源点到汇点的最长路径长度(关键路径)
- 关键路径上的活动:关键活动



最长时间与最短时间相减为0的为关键路径节点(即相等),关键活动
链接:https://blog.csdn.net/mgsky1/article/details/78124565
最短路径算法
- dijkstra算法(单源最短路径算法)


代码:

注意:迪杰斯特拉算法的权值不能为负数
- Floyd算法(各顶点之间最短路径)
适用范围:无负权回路即可,边权可正可负,运行一次算法即可求得任意两点间最短路。
基本思想:
弗洛伊德算法定义了两个二维矩阵:
矩阵D记录顶点间的最小路径
例如D[0][3]= 10,说明顶点0 到 3 的最短路径为10;
矩阵P记录顶点间最小路径中的中转点
例如P[0][3]= 1 说明,0 到 3的最短路径轨迹为:0 -> 1 -> 3。
它通过3重循环,k为中转点,v为起点,w为终点,循环比较D[v][w] 和 D[v][k] + D[k][w] 最小值,如果D[v][k] + D[k][w] 为更小值,则把D[v][k] + D[k][w] 覆盖保存在D[v][w]中。
- 结构定义:
1
2
3
4
5
6typedef struct struct_graph{
char vexs[MAXN];
int vexnum;//顶点数
int edgnum;//边数
int matirx[MAXN][MAXN];//邻接矩阵
} Graph; - 核心算法代码汇总:https://blog.csdn.net/o1101574955/article/details/44223917/
1
2
3
4
5
6
7
8
9
10
11
12
13
14//这里是弗洛伊德算法的核心部分
//k为中间点
for(k = 0; k < G.vexnum; k++){
//v为起点
for(v = 0 ; v < G.vexnum; v++){
//w为终点
for(w =0; w < G.vexnum; w++){
if(D[v][w] > (D[v][k] + D[k][w])){
D[v][w] = D[v][k] + D[k][w];//更新最小路径
P[v][w] = P[v][k];//更新最小路径中间顶点
}
}
}
}查找
静态查找表
一种优化:带哨兵(防止下标越界,提高效率)
代码如下:从后往前查找
1 | int Sequential_Search2(int *a int n,int key) |
成功平均查找长度:(n+1)/2
失败平均查找长度: n+1
有序表查找
折半查找
代码:
1 | int search(keytype key[],int n,keytype k) |
复杂度:O(log2n)
- 以上算法只适用于关键字顺序递增的有序表查找。如果该顺序表是关键字递减的,则算法需要改动,在low指针与high指针的修改上对调即可。
- 查找成功的最多比较次数:[log2(n+1)],失败的次数为[log2(n+1)]
索引顺序表查找算法(分块查找算法)
算法背景
有时候,可能会遇到这样的表:整个表中的元素未必有序,但若划分为若干块后,每一块中的所有元素均小于(或大于)其后面块中的所有元素。我们称这种为分块有序。对于分块有序表的查找
首先,我们需要先建立一个索引表,索引表中为每一块都设置–索引项,每一个索引项都包含两个内容:
该块的起始地址
该块中最大(或最小)的元素查找过程
在前面建立的索引表的基础上,我们查找一个关键字需要两个步骤:
在索引表中查找,目的是找出关键所属的块的位置。这里如果索引表较大的话,可以采用折半查找。
进入该块中,使用简单顺序表查找算法进行关键字查找。算法分析
分块查找的平均查找长度为ASLbs = Lb+Lw, 其中Lb为查找索引表确定所在块的平均查找长度,Lw为在块中查找元素的平均查找长度。
一般情况下,为进行分块查找,可以将长度为n的表均匀地分成b块,每块含有s个记录,即b=[n/s];又假定表中每个记录的查找概率相等,则每块查找的概率为1/b,块中每个记录的查找概率为1/s。
若用顺序查找确定所在块,顺序查找子表中的元素,则分块查找的平均查找长度为: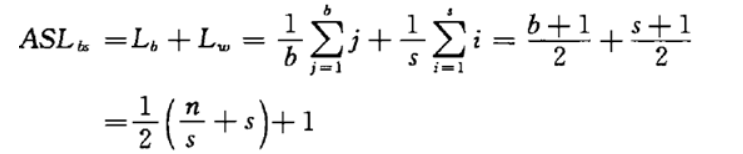
长度为n的线性表,分成$sqrt(n)$(根号n)查找次数最少
动态查找
- 二叉排序树
- 二叉平衡树
哈希函数法
- 直接定址法
- 质数除余法(取不超过表长的最大质数模)
- 平方取中法
解决冲突的方法: - 开放地址法(删除元素后再查找会造成问题)
用于顺序存储结构 - 拉链法:适用于经常进行删除操作的
- 装载因子:反映哈希表的饱和程度:n/m n为记录数,m为表长
排序
总览:
稳定类
插入排序
代码:
1 | //插入排序 |
平均时间复杂度:O(n^2),空间O(1),可适用于链式存储结构
折半插入排序
代码:
就是二分+插入的结合
复杂度与之前相同,只适用于顺序存储
归并排序
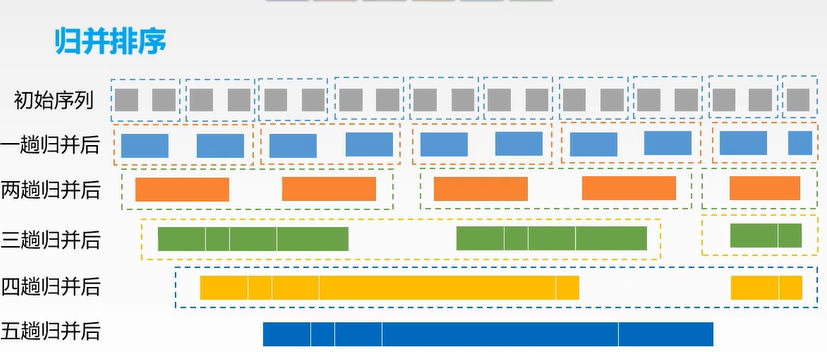
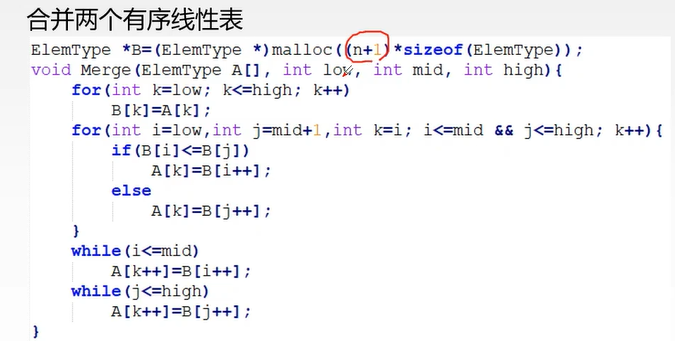

时间复杂度:nlog2n,空间:O(n)
基数排序
类似于桶排序,有分配和收集
个位,十位,百位,不基于比较
不稳定类
希尔排序(缩小增量排序)
选择排序
代码:
1 | //选择排序 |
比较O(n^2),移动最少O(1),最坏O(n)
空间O(1)
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
博客:https://www.cnblogs.com/chengxiao/p/6129630.html
完全二叉树最后一个非叶子节点下标为[n/2],n是节点总数堆排序步骤:
1、从k-1层的最右非叶结点开始,使关键字值大(或小)的记录逐步向二叉树的上层移动,最大(或小)关键字记录成为树的根结点,使其成为堆。
2、逐步输出根结点,令r[1]=ri,在将剩余结点调整成堆。直到输出所有结点。我们称这个自堆顶到叶子的调整过程为“筛选”。(3)要解决的两个问题:
1、如何由一个无序序列建成一个堆; 2、输出一个根结点后,如何将剩余元素调整成一个堆。 将一个无序序列建成一个堆是一个反复“筛选”的过程。若将此序列看成是一个完全二叉树,则最后一个非终端结点是第floor(n/2)个元素,由此“筛选”只需从第floor(n/2)个元素开始。 堆排序中需一个记录大小的辅助空间,每个待排的记录仅占有一个存储空间。堆排序方法当记录较少时,不值得提倡。当n很大时,效率很高。堆排序是不稳定的。代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78#include "iostream"
using namespace std;
#define MAXSIZE 20
typedef struct
{
int key;
//其他数据信息
}RedType;
typedef struct
{
RedType r[MAXSIZE+1];
int length;
}Sqlist;
typedef Sqlist HeapType; //堆采用顺序表存储表示
void HeapAdjust(HeapType &H,int s,int m) //已知H.r[s...m]中记录的关键字出H.r[s].key之外均满足堆的定义,本函数调整H.r[s]的关键字,使H.r[s...m]成为一个大顶堆(对其中记录的关键字而言)
{
int j;
RedType rc;
rc=H.r[s];
for(j=2*s;j<=m;j*=2) //沿key较大的孩子结点向下筛选
{
if(j<m && (H.r[j].key<H.r[j+1].key)) //j为key较大的记录的下标
++j;
if(rc.key>=H.r[j].key) //rc应插入在位置s上
break;
H.r[s]=H.r[j]; //将左、右孩子较大的结点与父节点进行交换,建成大顶堆
s=j;
}
H.r[s]=rc; //插入
}
void HeapSort(HeapType &H) //对顺序表H进行堆排序
{
int i;
for(i=H.length/2;i>0;--i) //由一个无序序列建成一个大顶堆,将序列看成是一个完全二叉树,则最后一个非终端节点是第n/2个元素
HeapAdjust(H,i,H.length);
for(i=H.length;i>1;--i)
{
H.r[0]=H.r[1]; //将堆顶记录和当前未经排序的子序列H.r[1...i]中最后一个记录相互交换
H.r[1]=H.r[i];
H.r[i]=H.r[0];
HeapAdjust(H,1,i-1); //将H.r[1...i-1]重新调整为大顶堆
}
}//HeapSort
void InputL(Sqlist &L)
{
int i;
printf("Please input the length:");
scanf("%d",&L.length);
printf("Please input the data needed to sort:\n");
for(i=1;i<=L.length;i++) //从数组的第1个下标开始存储,第0个下标作为一个用于交换的临时变量
scanf("%d",&L.r[i].key);
}
void OutputL(Sqlist &L)
{
int i;
printf("The data after sorting is:\n");
for(i=1;i<=L.length;i++)
printf("%d ",L.r[i].key);
printf("\n");
}
int main(void)
{
Sqlist H;
InputL(H);
HeapSort(H);
OutputL(H);
system("pause");
return 0;
}
复杂度:O(nlog2n),既适用于顺序,也适用于链式
快速排序
博客:https://blog.csdn.net/nrsc272420199/article/details/82587933
代码:
1 | Paritition1(int A[], int low, int high) { |


注意:当序列基本有序时,快速排序最不利于发挥长处,在每次划分得到两个长度基本相等的子文件时最易发挥长处
总结:







